题解 CF632F 【Magic Matrix】

发表于 | 更新于

定义一个大小为 $n\times n$ 矩阵 $a$ 为魔法矩阵，当且仅当 $a$ 满足以下条件:

以下 $i,j,k\in \mathbb{Z^+}$

  • $\forall i\in[1,n],a_{i,i}=0$

  • $\forall i,j\in[1,n],a_{i,j}=a_{j,i}$

  • $\forall i,j,k\in[1,n],a_{i,j}\le\max(a_{i,k},a_{j,k})$

给你一个矩阵，问它是不是魔法矩阵。

如果 $a$ 是魔法矩阵输出 $\texttt{MAGIC}$，否则输出 $\texttt{NOT MAGIC}$，可以参见样例。

$1\leq n\leq 2500,\forall i,j\in[1,n],0\le a_{i,j}\le 10^9$

最小生成树：

咋一看和最小生成树一点关系都没有，但是我们设$a_{i,j}$表示$i$到$j$的边的边权为$a_{i,j}$,然后观察本题的三个条件：

$1.$对于每一个$i,j,a_{i,j}=a_{j,i}$(说明是无向图)

$2.$对于每个$i,a_{i,i}=0$(表示没有自环)

$3.$对于每个$i,j,k$,都有$a_{i,j}\leqslant max(a_{i,k},a_{k,j})$

第三个条件说明的就是最小生成树

我们可以设$f_{i,j}$为$i$到$j$的任意路径的最长边的最小值，可得$a_{i,j}\geqslant f_{i,j}.$

假设一个矩阵满足条件,则$a_{i,j}\leqslant max(a_{i,k_1}~,~a_{k_1,k_2}),a_{k_1,j}\leqslant max(a_{k_1,k_2},a_{k_2,j})\cdots\cdots$

$∴a_{i,j}\leqslant max(a_{i,k_1},a_{k_1,k_2},a_{k_2,k_3},\cdots,a_{k_m,j})$

$=f_{i,j}$

判断矩阵是否合法，就是判断图上的$i$到$j$的任意路径的最长边的最小值是否等于$a_{i,j}$.

这可以用最小生成树实现,模拟一遍$Kruskal$会更好理解，从最小的边开始加，形成环显然走已经形成的路更优，加边到形成树就保证图联通了就没必要加边了

判断合法即判断完全图中是不是任意一个生成树都是最小生成树

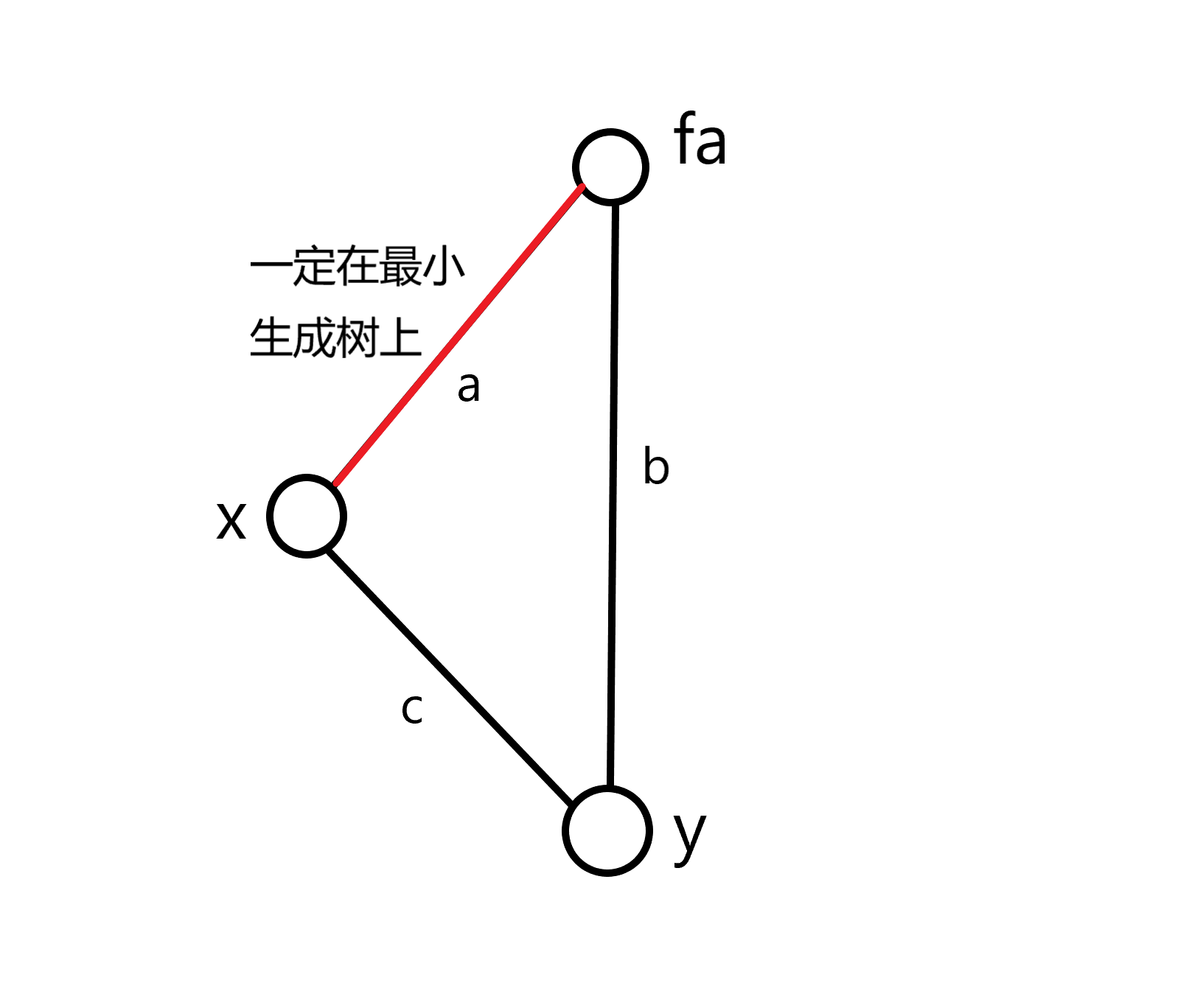
具体实现就是以任意一个节点(我使用$1$)为根，记录每个节点的父节点$fa$,然后找一个$y$,如下图，如果$max(a,b)<c$,那么就不符合最小生成树和题目给定条件了。

$Code$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<bits/stdc++.h>
#define re register
using namespace std;
inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
int n,a[2555][2555],vis[2555],dis[2555],fa[2555],dep[2555];
int main(){
    int n=read();
    for(re int i=1;i<=n;i++)
        for(re int j=1;j<=n;j++)a[i][j]=read();
    for(re int i=1;i<=n;i++)
        if(a[i][i]){
            puts("NOT MAGIC\n");
            return 0;    
        }
    for (re int i=1;i<=n;++i)
        for (re int j=1+i;j<=n;++j)
            if (a[i][j]!=a[j][i]){
                puts("NOT MAGIC");
                return 0;    
                }
    for (re int i=0;i<=n;++i)fa[i]=i,dis[i]=1e9+1e8;dis[1]=0;
       for (re int i=1;i<=n;++i){
           re int pos=0;
           for (re int j=1;j<=n;++j)    
               if (!vis[j]&&dis[pos]>dis[j])
                   pos=j;
           vis[pos]=1;
           for (re int j=1;j<=n;++j)
               if (!vis[j]&&a[pos][j]<dis[j])
                   dis[j]=a[pos][j],fa[j]=pos,dep[j]=dep[pos]+1;    
    }
    for (re int i=1;i<=n;++i)
        for (re int j=1;j<=n;++j){
            re int x=i,y=j;
            if (max(a[x][fa[x]],a[fa[x]][y])<a[x][y])
                return puts("NOT MAGIC"),0;
            if (max(a[x][fa[y]],a[fa[y]][y])<a[x][y])
                return puts("NOT MAGIC"),0;
        }
    puts("MAGIC");
    return 0;
}